GAMES101 Lecture 18 - Advanced Topics in Rendering

GAMES101_Lecture_18.pdf

Outline

• Advanced light transport and materials

• Mostly FYI

I. Advanced Light Transport

• Unbiased light transport methods

  • Bidirectional Path Tracing (BDPT)

  • Metropolis Light Transport (MLT)

• Biased light transport methods

  • Photon Mapping

  • Vertex Connection and Merging (VCM)

• Instant Radiosity (VPL or Many light methods)

Biased vs. Unbiased Monte Carlo Estimators

• An unbiased Monte carlo technique does not have any systematic error

  • The expected value of an unbiased estimator will always be the correct value, regardless of the number of samples used

• Otherwise, biased

  • One special case, the expected value converges to the correct value as infinite #samples are used - consistent

Unbiased Light Transport Methods

Bidirectional Path Tracing (BDPT)

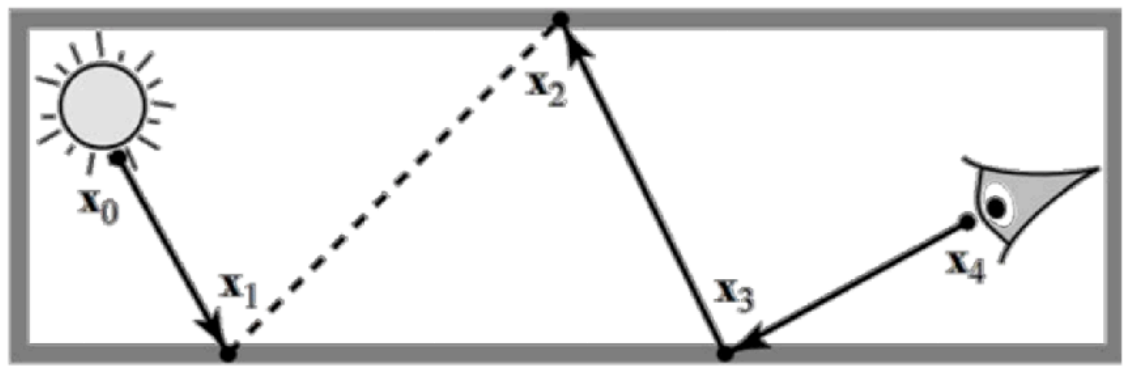
• Trace sub-paths from both the camera and the light

• Connects endpoints from both sub-paths

Pros

• Suitable if the light transport is complex on the light's side

  • Similar to precomputing for the light source

Cons

• Difficult to implement & quite slow

Metropolis Light Transport (MLT)

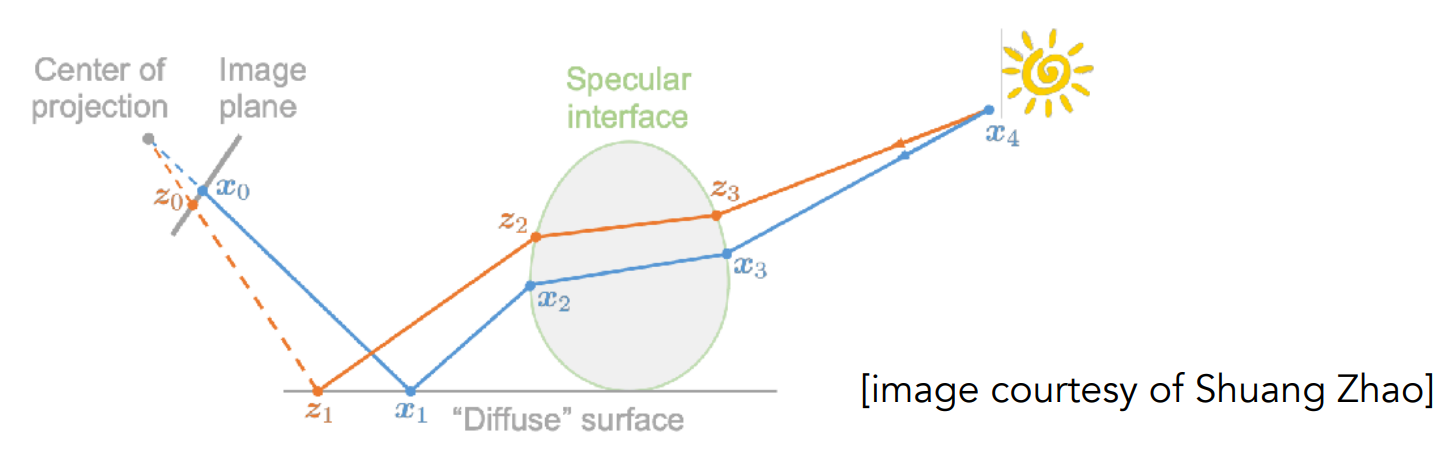
• A Markov Chain Monte Carlo (MCMC) application

  • Jumping from the current sample to the next with some PDF

  • Application of MCMC leads to a series of generated samples whose distribution exactly matches the target function to be integrated, resulting in the minimum variance.

• Very good at locally exploring difficult light paths

• Key idea

  • Locally perturb an existing path to get a new path

Pros

• Works great with difficult light paths

  • Specular-Diffuse-Specular path, SDS path

Cons

• Difficult to estimate the convergence rate

• Does not guarantee equal convergence rate per pixel, because MCMC is for local sampling

  • Usually produces "dirty" results

Biased Light Transport Methods

Photon Mapping

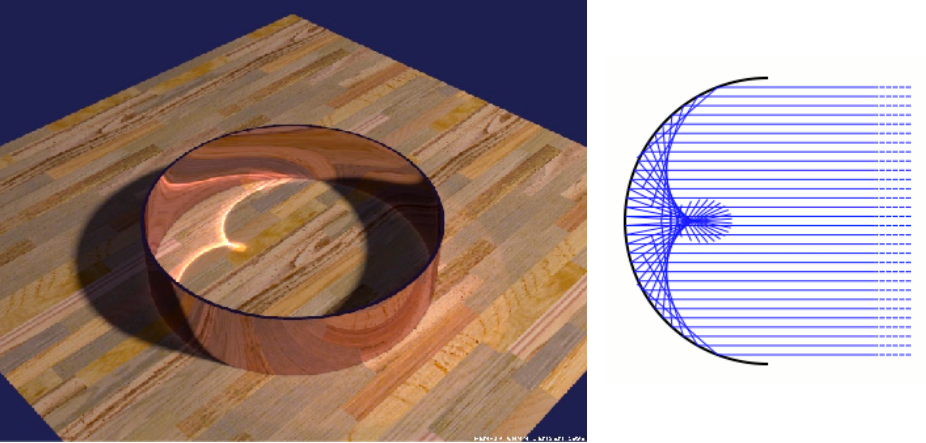
• A biased approach & A two-stage method

• Very good at handling Specular-Diffuse-Specular (SDS) paths and generating caustics

  • Caustics refer to the visible pattern caused by the focusing or concentration of light or other waves as they pass through or reflect off a curved or irregular surface. It is commonly observed as bright or dark patches, streaks, or rippling patterns in the vicinity of the surface.

Approach (Variations Apply)

Stage 1 - Photon Tracing

• Emitting photons from the light source, bouncing them around, then recording photons on diffuse surfaces

  

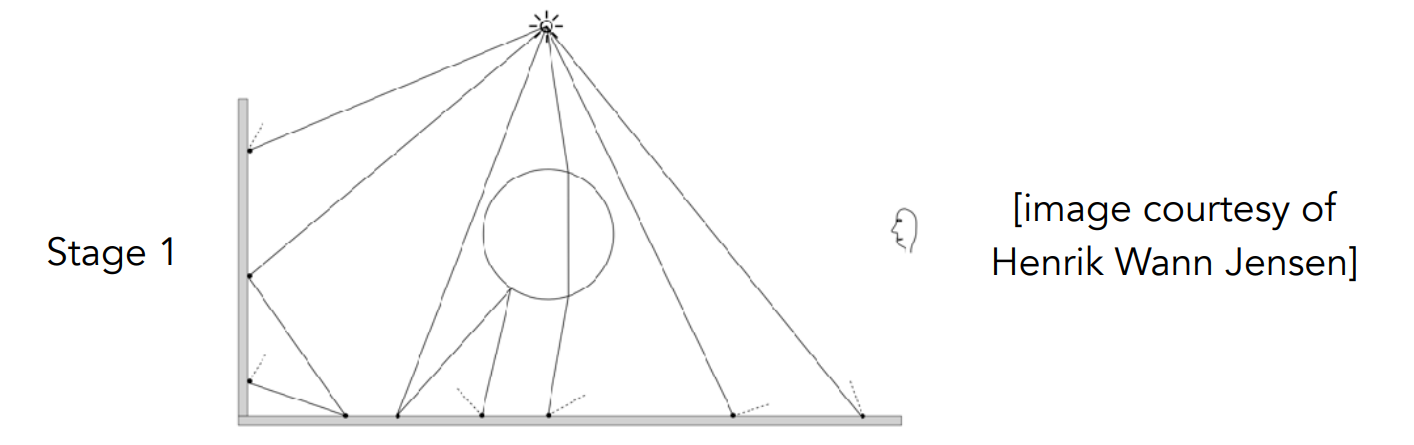
Stage 2 - Photon Collection

• Shoot sub-paths from the camera, bouncing them around, until they hit diffuse surfaces

Calculation - Local Density Estimation

• Idea: areas with more photons should be brighter

• For each shading point, find the nearest $N$$N$ photons. Take the surface area they cover

  • K-Nearest Neighbour Clustering

• Compute the density of the photons

Why biased?

• Local density estimation isn't correct

  $$\frac{\mathrm{d}N}{\mathrm{d}A}\ne \frac{\mathrm{\Delta }N}{\mathrm{\Delta }A}$$

• But in the sense of limit,

  • More photons emitted implies

    • the same $N$$N$ photons covers a smaller $\mathrm{\Delta }A$$\Delta A$

      • $\mathrm{\Delta }A$$\Delta A$ is closer to $\mathrm{d}A$$\dd{A}$

• Biased, but consistent

• Understanding biases in rendering:

  • Biased == Blurry

  • Consistent == Not blurry with infinite #samples

• Why not do a "const range" search for density estimation?

  • Results in inconsistency (not converging)

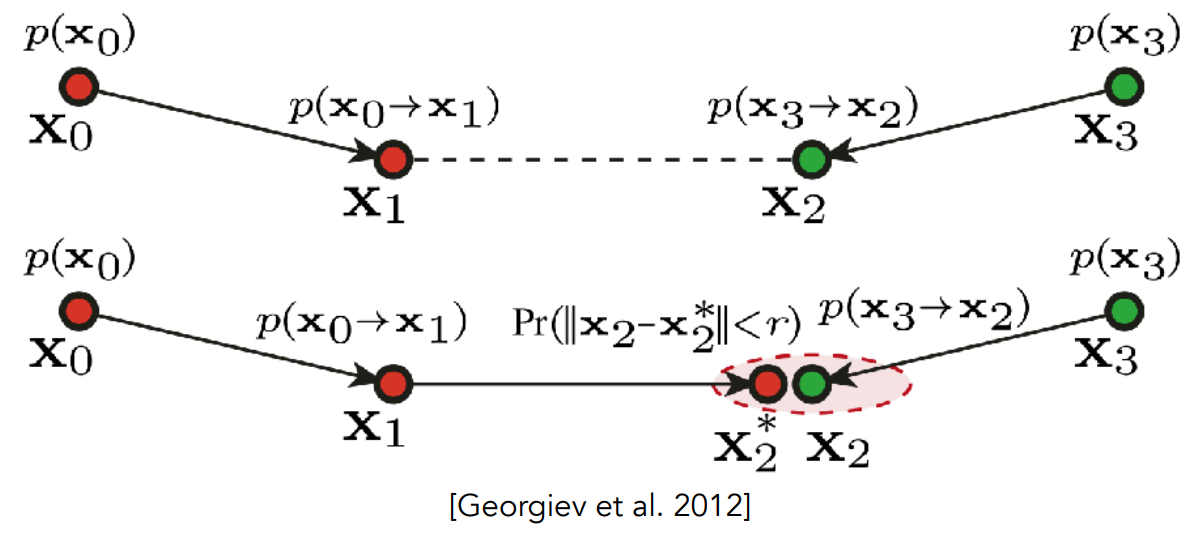
Vertex Connection and Merging (VCM)

• A combination of BDPT and Photon Mapping

• Key idea:

  • Utilize those unused sub-paths in BDPT if their endpoints cannot be connected but can be merged

  • Use photon mapping to handle the merging of nearby "photons"

• Adapted in the movie industry

Instant Radiosity (IR)

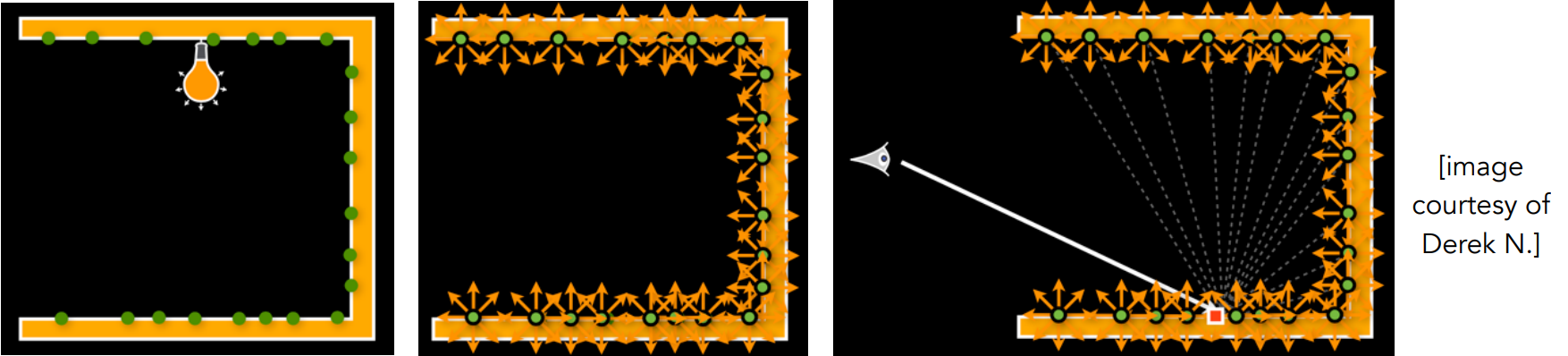
• Also called many-light approaches

• Key idea:

  • -Lit surfaces can be treated as light sources

Approach

• Shoot light sub-paths and assume the endpoint of each sub-path is a Virtual Point Light (VPL)

  • They stop at diffuse surfaces

• Render the scene as usual using these VPLs

Pros

• Fast and usually gives good results on diffuse scenes

Cons

• Spikes will emerge when VPLs are close to shading points

  • Related to the inverse quadratic term ($1/R^2$$1 / R^2$) when computing BSDF

• Cannot handle glossy materials

Industrial Use

Industry often uses path-tracing.

II. Advanced Apperance Modeling

Outline

• Non-surface models

  • Participating Media

  • Hair/Fur/Fiber (BCSDF)

  • Granular Material

• Surface Models

  • Translucent Material (BSSRDF)

  • Cloth

  • Detailed Material (Non-statistical BRDF)

• Procedural Appearance

Non-Surface Models

Participating Media

Examples

Fog

Definition

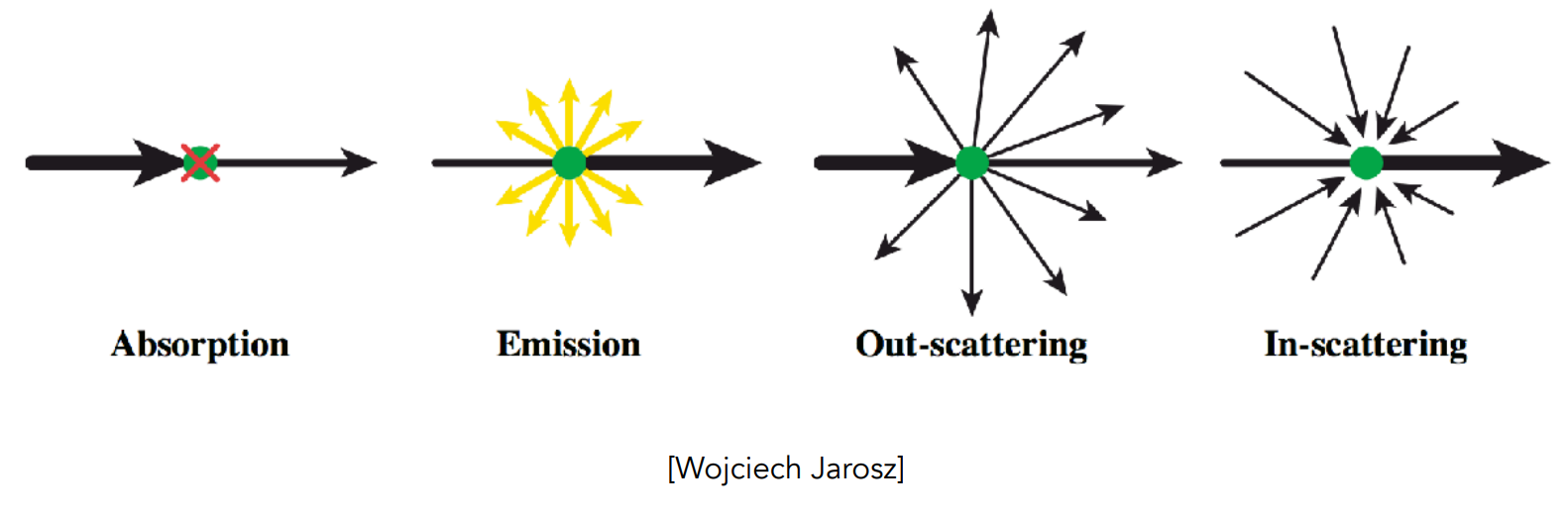
• At any point as ligh travels through a participating medium, it can be (partially) absorbed and scattered

  

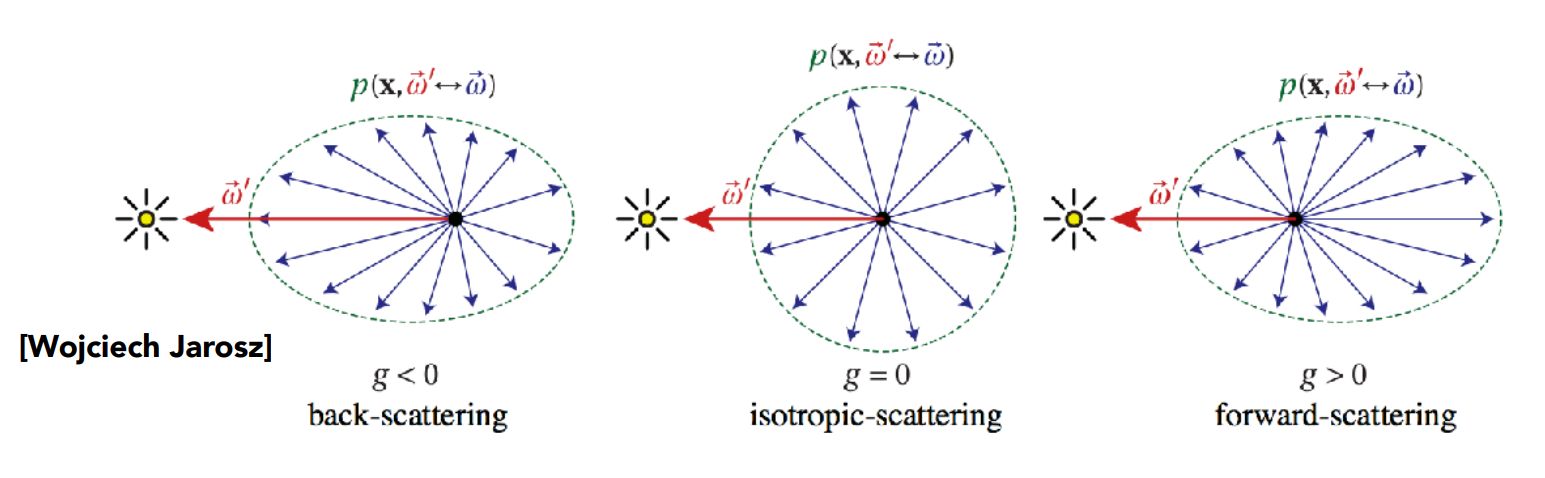
• Use Phase Function to describe the angular distribution of light scattering at any point $x$$x$ within participating media

  

Rendering

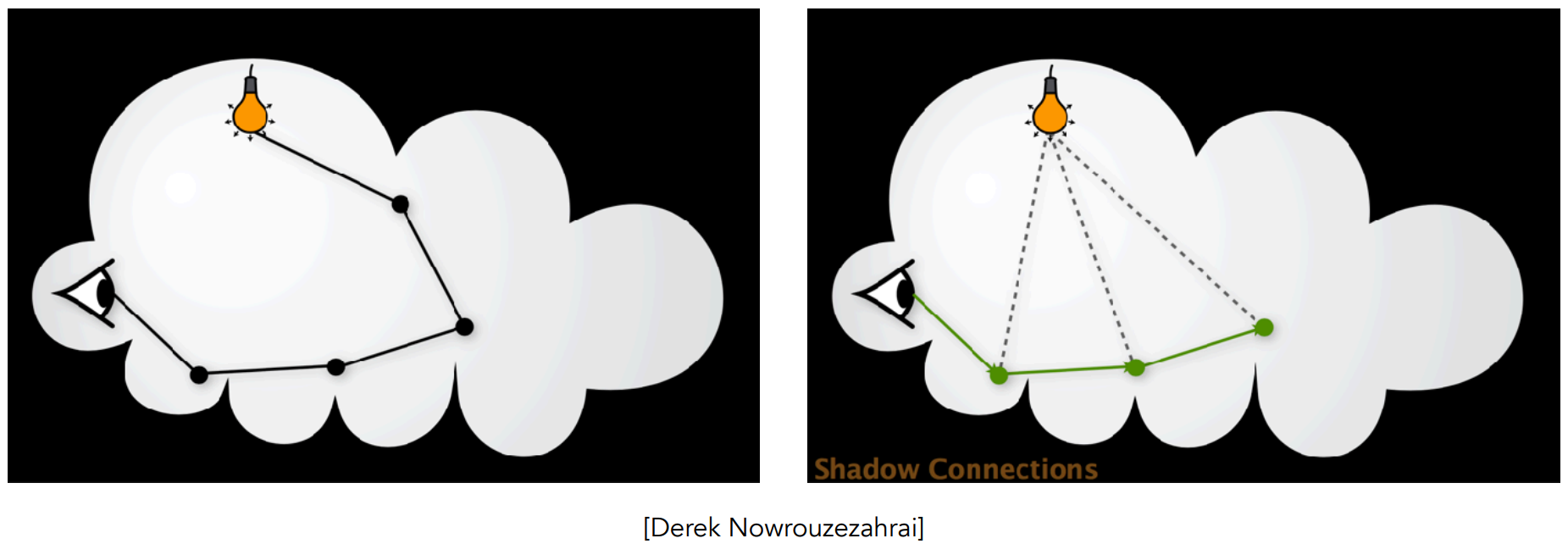
• Randomly choose a direction to bounce

• Randomly choose a distance to go straight

• At each "shading point", connect to the light

Hair/Fur/Fiber (BCSDF)

Hair Appearance

• Colored highlights

• Uncolored highlights

Kajiya-Kay Model

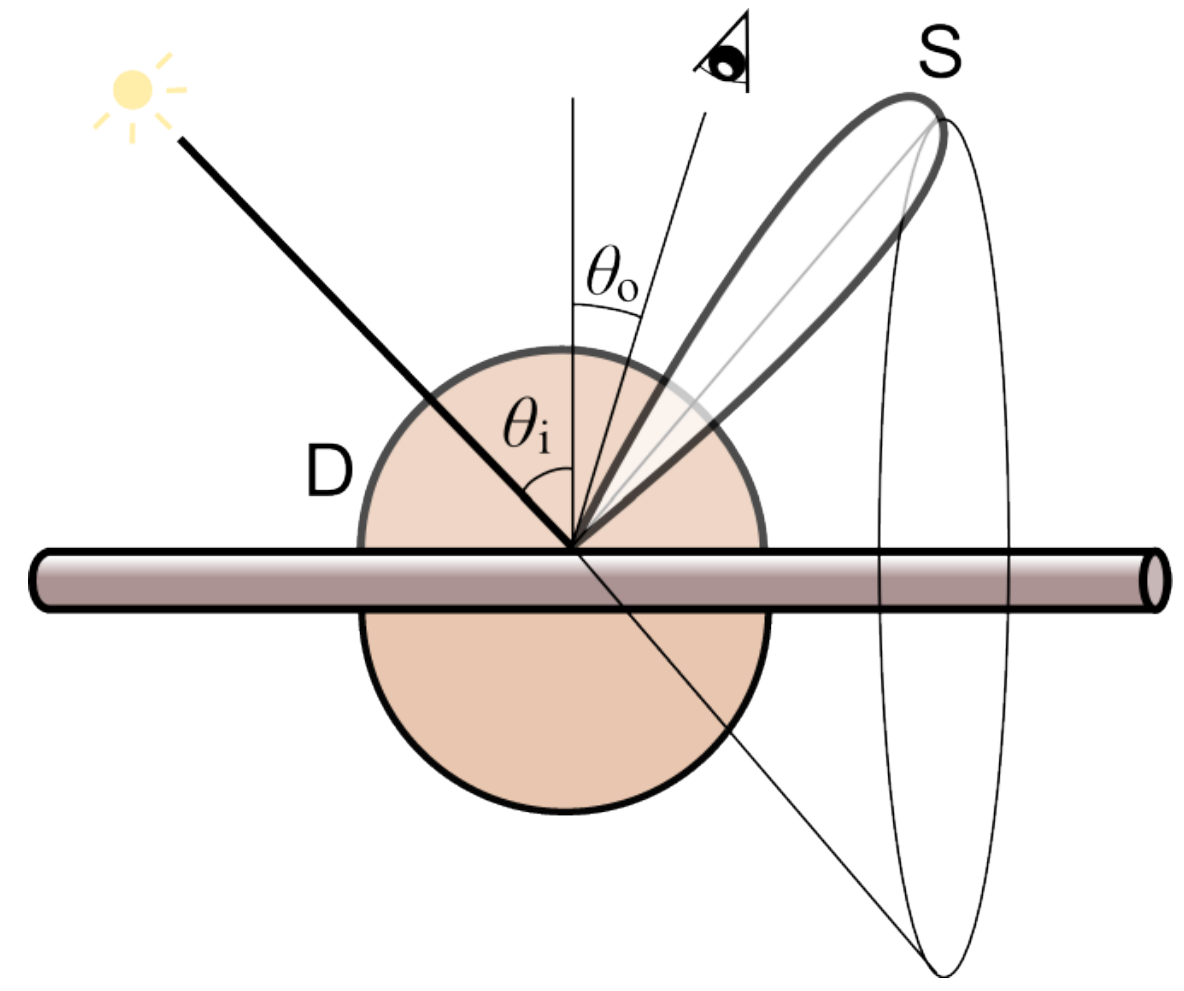
• Model the hair as a cylinder

• When light hits the cylinder, it is diffused

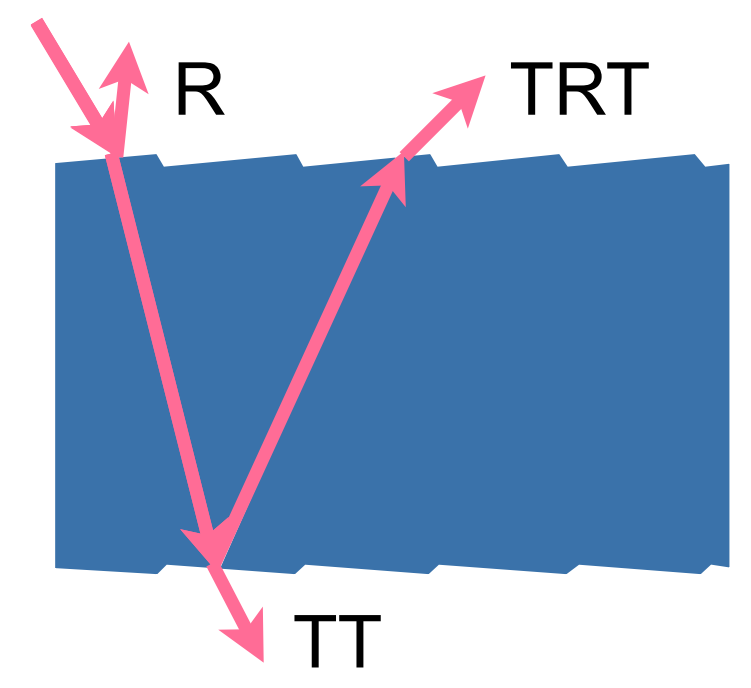
Marschner Model

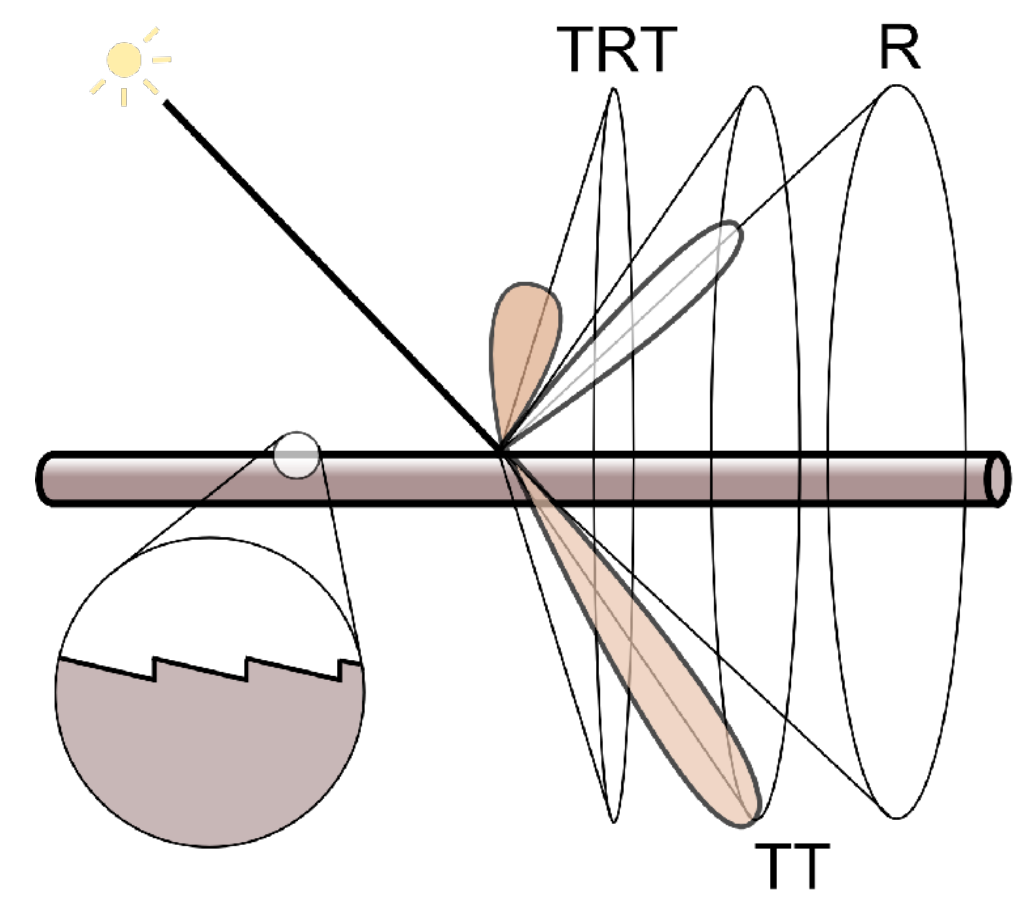
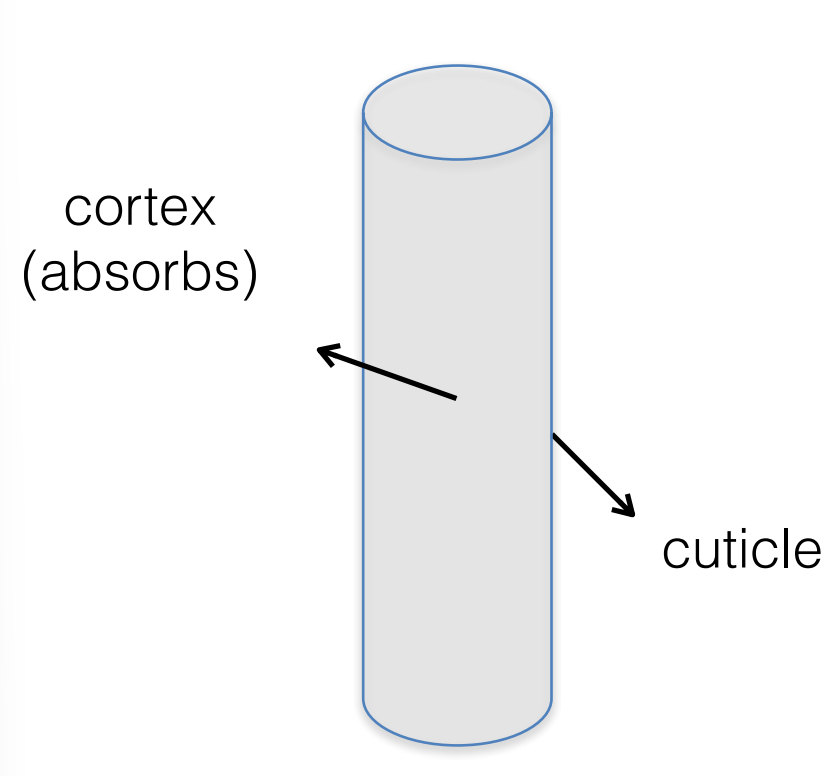
• Glass-like cylinder

  • Outside: Cuticle

  • Inside: Cortex, colored, partial light absorbtion

  

• 3 types of light interactions: $R$$R$, $TT$$TT$, $TRT$$TRT$, where $R:\text{Reflection}$$R: \text{Reflection}$, $T:\text{Transmission}$$T: \text{Transmission}$

  

Fur Appearance

• Cannot realize the diffusive and saturated appearance if represented as human hair

Human Hair vs Animal Fuir

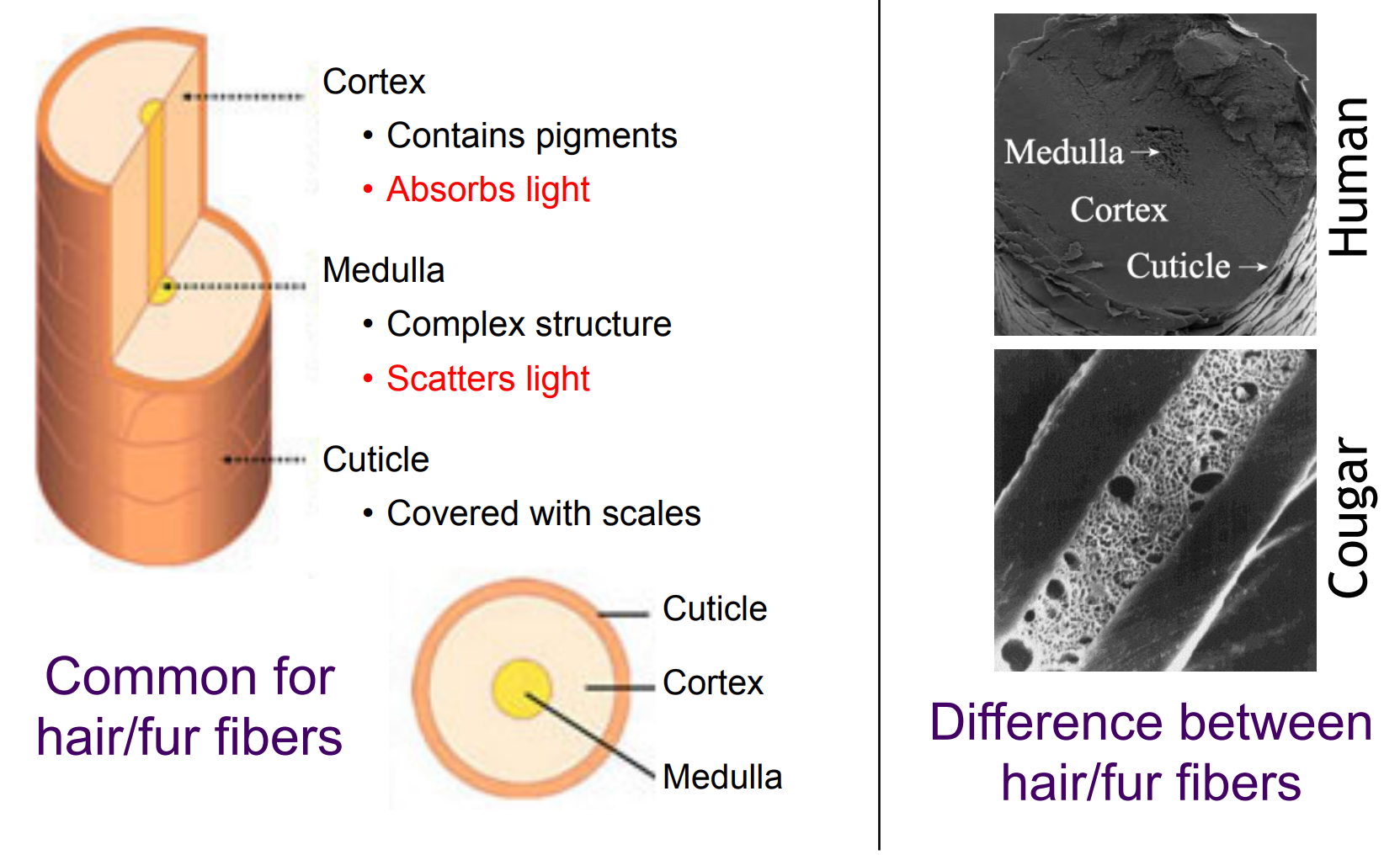
Structural:

• Similarity: Cuticle, Cortex, Medulla

• Difference:

  • Fur has its medulla significantly larger

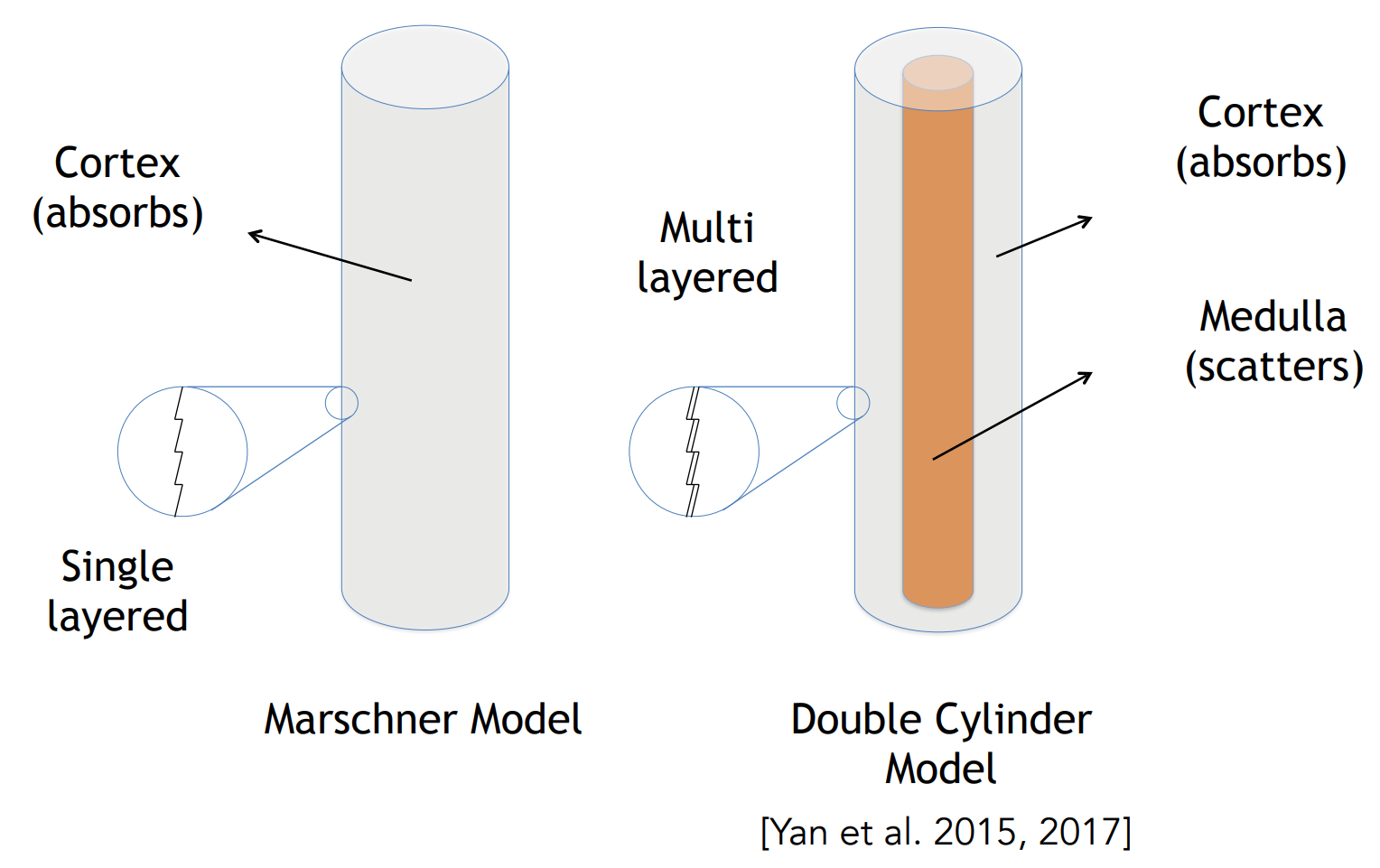
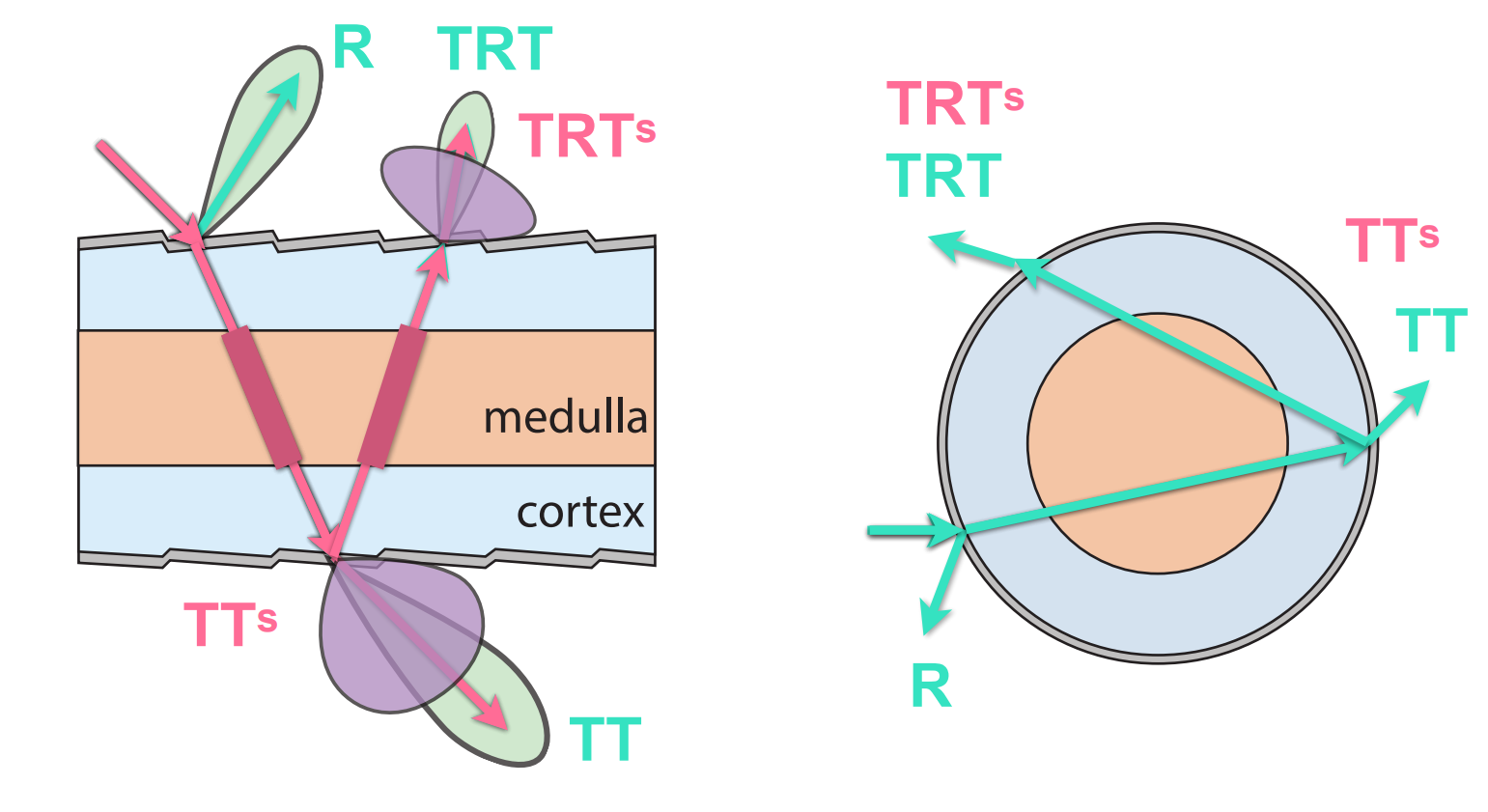
Importance of Medulla in Human Hair

Double Cylinder Model

• $s$$s$ - scattering

Granular Material

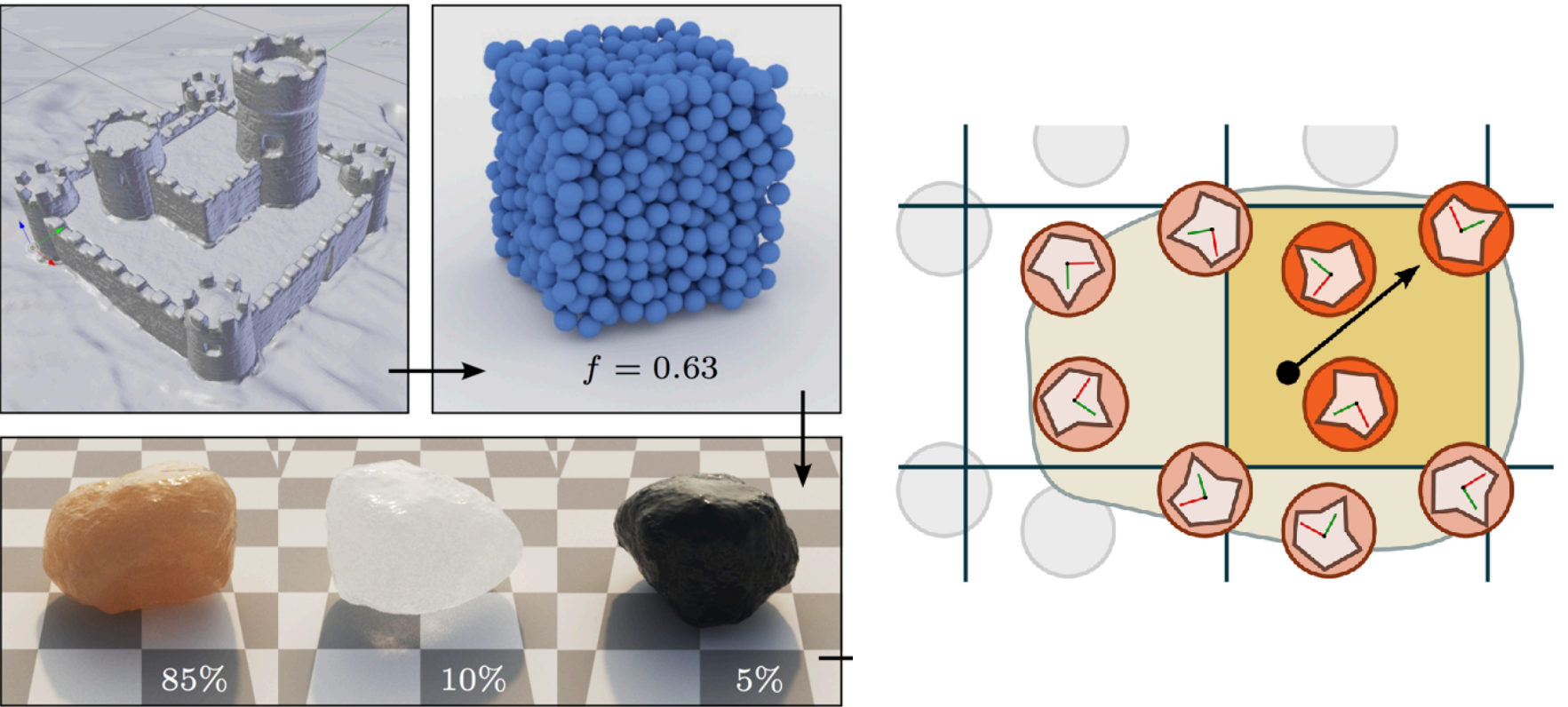
Procedural Definition

• Define basic units for construction

Surface Models

Translucent Material

Material	Example
Jade
Jellyfish

Translucent: Both scattering and absorption

Subsurface Scattering

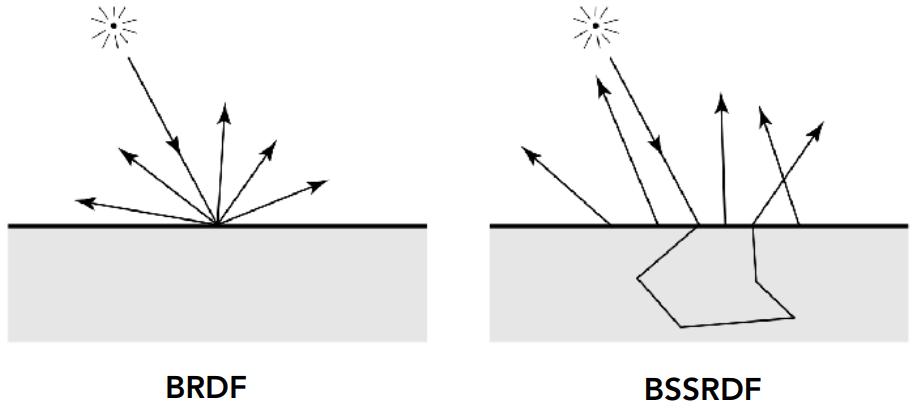
Subsurface Scattering: Visual characteristics of many surfaces caused by light exiting at points different from which it enters at.

• Violates a fundamental assumption of the BRDF

Scattering Functions

BSSRDF (Subsurface Scattering): generalization of BRDF; exitant radiance at one point due to incident differential irradiance at another point:

• Generalization of rendering equation: integrating over all points on the surface and all directions

  $$L(x_o,{\omega }_o)={\int }_A{\int }_{H^2}S(x_i,{\omega }_i,x_o,{\omega }_o)L_i(x_i,{\omega }_i)\cos {\theta }_i\mathrm{d}{\omega }_i\mathrm{d}A$$

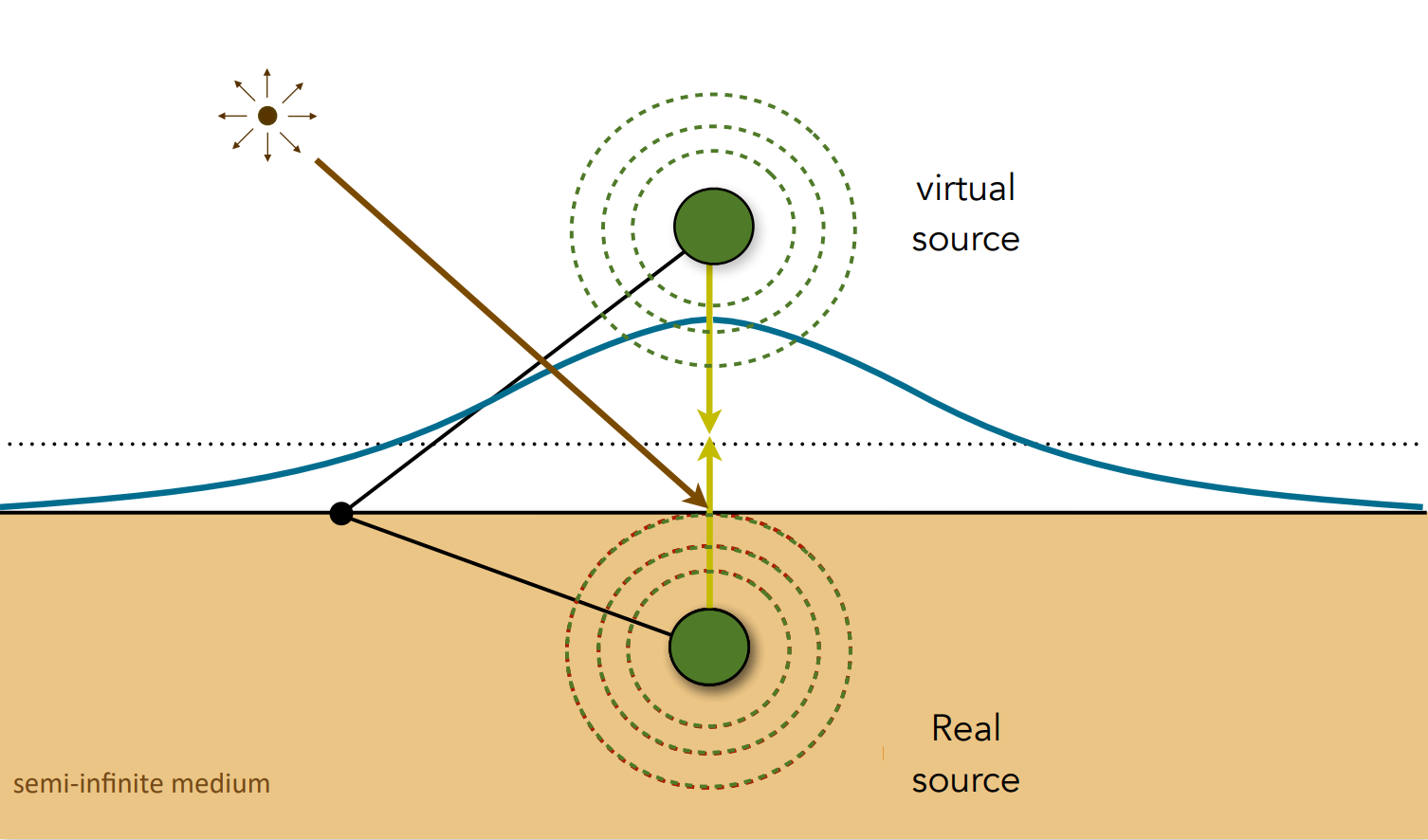
Dipole Approximation

• Apprximate light diffusion by introducting two point sources

Cloth

• A collection of twisted fibers

• Two levels of twist

  

• Woven or knitted

  

Render as Surface

• Given the weaving pattern, calculate the overall behavior

• Cannot simulate materials such as velvet

Render as Participating Media

• Properties of individual fibers & their distribution -> scattering parameters

• Render as a participating medium

Render as Actual Fibers

• Render every fiber explicitly

Detailed Appearance

Motivation: Real world is more complicated

Not always perfect.

Microfacet BRDF

Surface = Specular microfacets + statistical normals

• Distribution of Normals should match that in the reality

  • Normal Distribution Function, NDF

• Path sampling is difficult

  • Hard to find a path that connects the camera and the light source

BRDF over A Pixel

• Compute normals inside the area where a pixel is projected to

Recent Trend: Wave Optics

Procedural Appearance

Procedure: When needed, just compute

• Define details without textures

  • Compute a noise function on the fly

  • 3D noise -> internal structure if cut or broken

Perlin Noise

• Generate structures