GAMES101 Lecture 15 - Ray Tracing 3 (Light Transport and Global Illumination, with Review on Probability)

GAMES101_Lecture_15.pdf

I. Radiometry Cont.

Please refer to Lecture14.md.

II. Bidirectional Reflectance Distribution Function (BRDF)

Reflection at a Point

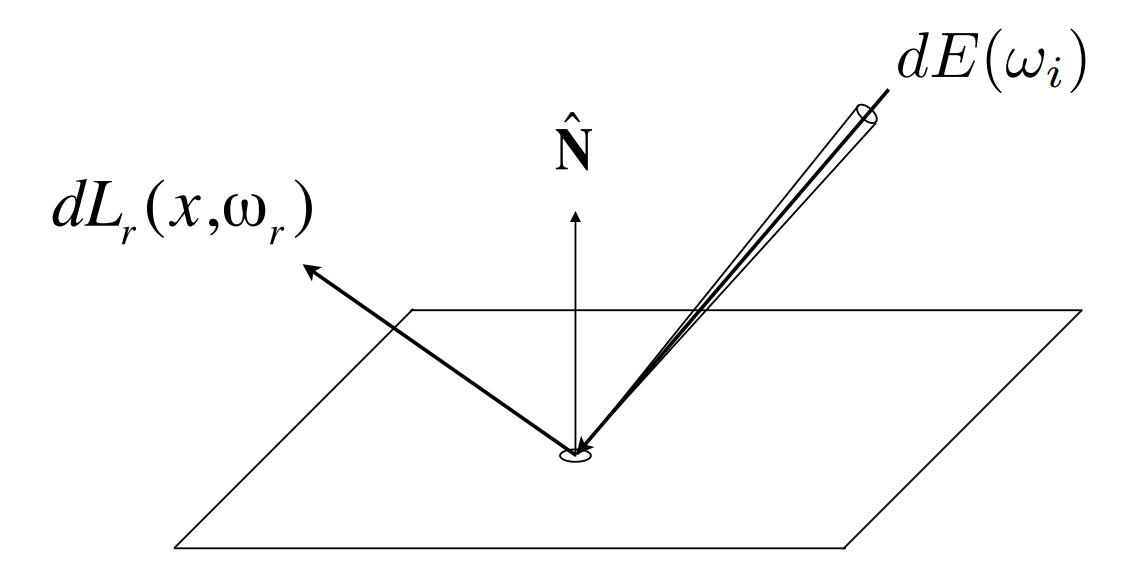
Radiance from direction ${\omega }_i$$\omega_i$ turns into the power $E$$E$ that $\mathrm{d}A$$\dd{A}$ receives. Then the power $E$$E$ will be come the radiance to any other direction ${\omega }_o$$\omega_{o}$.

• Differential radiance incoming:

  $$\mathrm{d}E({\omega }_i)=L({\omega }_i)\cos {\theta }_i\mathrm{d}{\omega }_i$$

• Differential radiance exiting due to $\mathrm{d}E({\omega }_i)$$\dd{E(\omega_i)}$:

  $$\mathrm{d}{L}_r({\omega }_r)$$

BRDF

The Bidirectional Reflectance Distribution Function (BRDF) describes how much light is reflected into each outgoing direction ${\omega }_r$$\omega_r$ from each incoming direction ${\omega }_i$$\omega_i$.

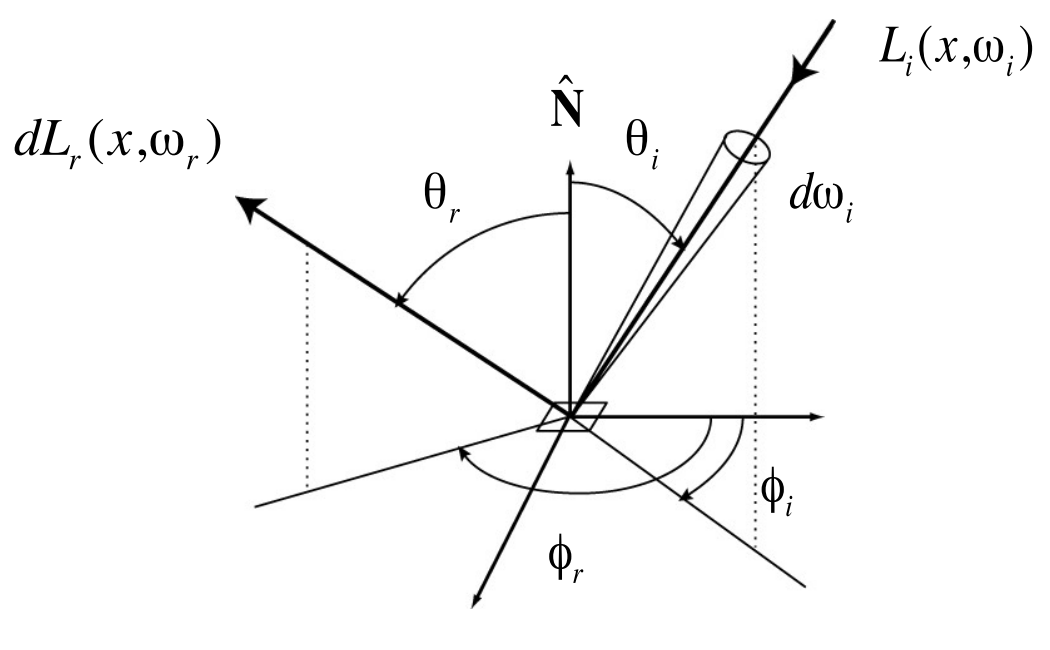
The Reflection Equation:

In this equation, what we do is essentially summing up the contributions to this particular outgoing direction ${\omega }_r$$\omega_r$ from all other directions, by doing integration on the entire hemisphere. The differential part on the right side, is acquired by multiplying BRDF with the differential of the irradiance.

Challenge: Recursive Equation

• Incoming radiance depends on reflected radiance, at another point in the scene

III. The Rendering Equation

The Rendering Equation

Adding an emission term on equation $\text{1}$$\ref{refleq}$ gives the rendering equation:

where $p$$p$ is the point being considered, and ${\mathrm{\Omega }}_{+}$$\Omega_{+}$ denotes the upper hemisphere.

• All directions are pointing outwards, e.g. ${\omega }_i$$\omega_i$.

• Why can we directly do an integration? From the linearity.

Transforming the Rendering Equation

Rendering Equation as Integral Equation

Equation $\text{2}$$\ref{rendeq}$ is a Fredhold Integral Equation of second kind (extensively studied numerically) with canonical form:

Linear Operator Equation

Equation $\text{3}$$\ref{fredhold}$ can be further transformed by applying the Light Transport Operator.

which can be then discretized to a simple matrix equation, where:

• $L$$L$, $E$$E$ are vectors, and

• $K$$K$ is the light transport matrix.

P.S. WTF? TODO: Needs further explanation.

Simplifying the Linear Operator Equation

Those expanded terms has physical meanings:

• $E$$E$ - Emission directly from light sources

• $KE$$KE$ - Direct illumination on surfaces

• $K^{2}E$$K^2E$ - Indirect illumination, one bounce

• $K^{3}E$$K^3E$ - Two bounces

• ...

Ray Tracing and Rasterization

Shading in rasterization is equivalent to solving the rendering equation using zero bounces.

Type	Effect
Direct Illumination
One-bounce global illumination
Two-bounce global illumination
Four-bounce global illumination
Eight-bounce global illumination
Sixteen-bounce global illumination

• Why the lantern is light/dark in some rendered results?

  • Light cannot escape the lantern only after several bounces (so that it reaches an illuminated surface)

• Is the result guaranteed to converge if an infinity number of passes can be calculated?

Appendix A: Review on Probability

• Random Variable

• Probability Density/Distribution Function, PDF

• Expected Value

• Function of a Random Variable

  $$E[Y]=E[f(x)]=\int f(x)p(x)\mathrm{d}x$$