GAMES101 Lecture 11 - Geometry 2 (Curves and Surfaces)

GAMES101_Lecture_11.pdf

I. Explicit Representations of Geometry

Refer to Lecture10.md.

II. Curves

Bézier Curve

• Evaluating Bézier Curves: de Casteljau Algorithm

  • Intuitive Procedure:

    • Repeat linear interpolation on adjacent points for parameter $t\in [0,1]$$t \in [0, 1]$ until there is only one point left.

    • On each iteration, reduce the number of points to be evaluated by 1.

    

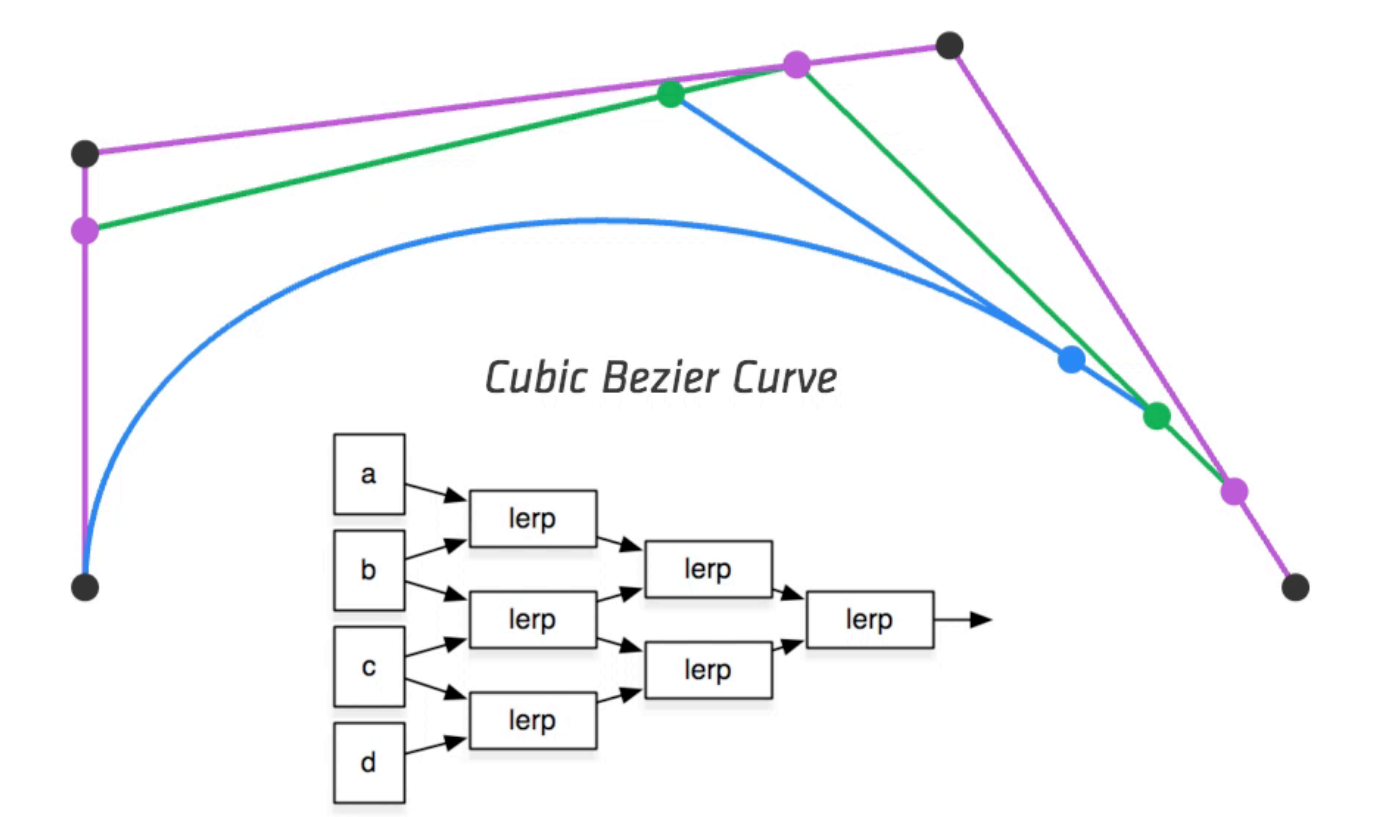
  • Algebraic Formula:

    Bernstein form of a Bézier curve of order $n$$n$:

    $${\mathbf{\text{b}}}^n(t)={\mathbf{\text{b}}}_t^n(t)=\sum _{j=0}^n{\mathbf{\text{b}}}_j{B}_j^n(t)$$

    where the Bernstein polynomial $B_j^n$$B^n_j$ is

    $$B_i^n(t)=(\genfrac{}{}{0ex}{}{n}{i})t^i(1-t{)}^{n-i}$$

    Similar to the binomial expansion.

• Properties:

  • Endpoint interpolation: Endpoints must be on the curve

  • Tangent to end segments: In the cubic case, ${\mathbf{\text{b}}}^{\prime }(0)=3({\mathbf{\text{b}}}_1-{\mathbf{\text{b}}}_0)$$\textbf{b}'(0) = 3(\textbf{b}_1 - \textbf{b}_0)$, and ${\mathbf{\text{b}}}^{\prime }(1)=3({\mathbf{\text{b}}}_3-{\mathbf{\text{b}}}_2)$$\textbf{b}'(1) = 3(\textbf{b}_3 - \textbf{b}_2)$

  • Affine transformation property: The curve can be transformed by transforming control points

  • Convex hull property: The curve is within convex hull of control points

Piecewise Bézier Curves

• Piecewise Cubic Bézier: the most common technique

  • Continuity:

    • $C^0$$C^0$ continuity: ${\mathbf{\text{a}}}_n={\mathbf{\text{b}}}_0$$\textbf{a}_n = \textbf{b}_0$

    • $C^1$$C^1$ continuity: ${\mathbf{\text{a}}}_n={\mathbf{\text{b}}}_0=\frac{1}{2}({\mathbf{\text{a}}}_{n-1}+{\mathbf{\text{b}}}_1)$$\textbf{a}_n = \textbf{b}_0 = \frac{1}{2} (\textbf{a}_{n-1} + \textbf{b}_1)$

    • ...

Splines (样条)

• Spline: A continuous curve constructed so as to pass through a given set of points and have a certain number of continuous derivatives.

  • A curve under control

• B-Spline: Short for basis splines.

  • Require more information than Bézier curves

  • Superset of the Bézier curves

  • Locality

III. Surfaces

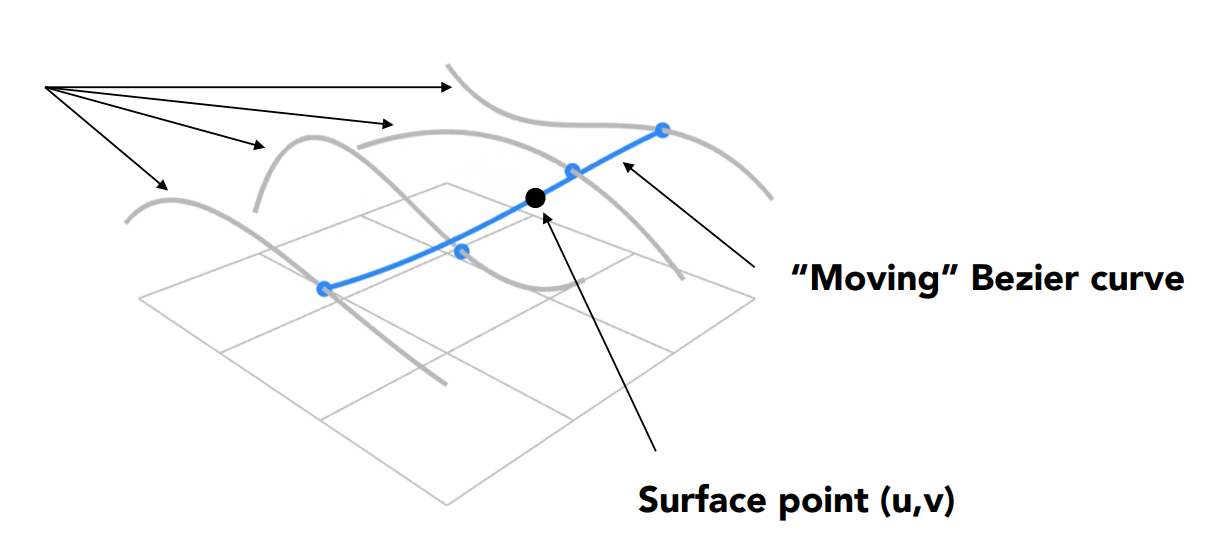
Bézier Surfaces

• Created by interpolating Bézier curves on two axes.

  

Mesh Operations: Geometry Processing

Refer to Lecture11.md.

Note: Bézier curve and Anti-aliasing